（数学基礎1-2）・数の種類


数学の基礎のお勉強
第1章「命題と論証，数の世界」
第3講「数の種類」

「数学の基礎のお勉強」のシリーズの記事です。
更新をサボってました…
記事の意図は上のリンク先を参照してください。

中学校の数学までは，実数までしか扱っていません。
高校に入り，数学IIの最初まで学ぶと新たな数である「複素数」を学びます。

さて，複素数まで含めて，今まで学んできた数に関して正しく理解できているでしょうか？
次の問題を見てみましょう。

問題

$\mathbb{N,~Z,~Q,~R,~C}$ はそれぞれ自然数，整数，有理数，実数，複素数全体の集合を表すものとする。(1) 〜 (5) に関しては，空欄にあてはまるものとして最も適切なものを（選択肢1）の中から 1 つ選べ。ただし，同じ選択肢を何度用いてもよいものとする．(6) に関しては①，②の問いに答えよ。

(1) $\sqrt{3}~[\hspace{10mm}]~\mathbb{Q}$ である。
(2) $\mathbb{N} ~[\hspace{10mm}]~ \mathbb{Z}$ である。
(3) $\displaystyle \frac{\sqrt{4}}{2} ~[\hspace{10mm}]~ \mathbb{Q}$ である。
(4) $\mathbb{Z} ~[\hspace{10mm}]~ \mathbb{Q}$ である。
(5) $\mathbb{C} ~[\hspace{10mm}]~ \mathbb{R}$ である。

(6)
①　無理数の定義を答えよ。
②　$A$ を無理数全体の集合とする．また，集合 $X,~ Y$ について，$X$ が $Y$ の部分集合であるとき，集合 $Y \cap \overline{X}$ を $Y-X$ で表すとする。ただし，$\overline{X}$ は集合 $X$ の補集合を表す。①で述べた定義にもとづくと，\[ A = [\hspace{5mm} \mbox{ア} \hspace{5mm}] -  [\hspace{5mm}\mbox{イ}\hspace{5mm}] \]である。空欄ア，イに当てはまる最も適切なものを（選択肢2）の中から 1 つ選べ。1つずつ選べ。

（選択肢1）
$({\rm a})\in \hspace{4mm} ({\rm b})\notin \hspace{4mm} ({\rm c}) \ni \hspace{4mm} ({\rm d})\ni \hspace{-9pt}/ \hspace{4mm} ({\rm e})= \hspace{4mm} ({\rm f}) \subset \hspace{4mm} ({\rm g}) \supset$

 （選択肢2）
$({\rm n})~ \mathbb{N} \hspace{4mm} ({\rm z})~ \mathbb{Z} \hspace{4mm} ({\rm q})~  \mathbb{Q} \hspace{4mm} ({\rm r})~ \mathbb{R} \hspace{4mm} ({\rm c})~\mathbb{C}$


    知識事項整理

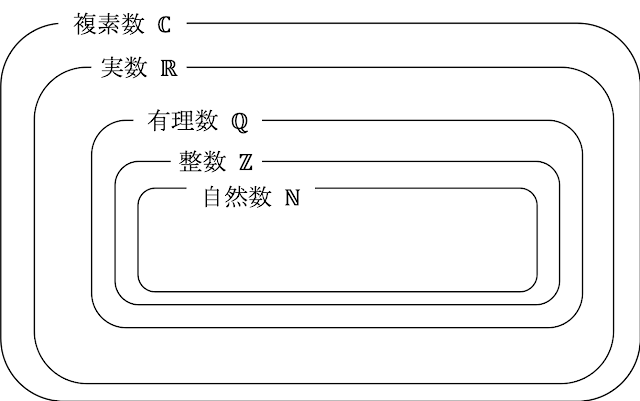
    さて，本問では「自然数」「整数」「有理数」「無理数」「実数」「複素数」という６種類の数が出てきます。それぞれの定義と関係は分かるでしょうか？
    それぞれ，ベン図で表すと以下の図のようになります。

    このようにして見ると，小学校の算数で習った「自然数」から徐々に概念を広げているのが分かると思います（小学校だと負の数を習わないので，厳密には違いますが…）。
    有理数の定義については，次回の記事で扱います。

    (6)では無理数はどの部分にあたるのかが問われていますね。
    上の図には登場していませんが，どこなのでしょうか…

    永島先生のポイント集（No. 1001）でも，非常に丁寧に説明がされているので，確認してみてください。

    というわけで，この問題の解答です。

    解答

    (1) $\sqrt{3}$ は無理数であるから $\sqrt{3} \notin \mathbb{Q}$ である．よって，答えは (b) ．

    (2) すべての自然数 $n$ について，$n \in \mathbb{Z}$ が成り立つから，$\mathbb{N}$ は $\mathbb{Z}$ の部分集合，すなわち $\mathbb{N} \subset \mathbb{Z}$ である．よって，答えは (f) ．

    (3) $\displaystyle \frac{\sqrt{4}}{2} = 2 \left( = \frac{2}{1} \right)$ より，$ \displaystyle \frac{\sqrt{4}}{2} \in \mathbb{Q}$ である．よって，答えは (a) ．

    (4) すべての整数 $n$ について，$n \in \mathbb{Q}$ が成り立つから，$\mathbb{Z}$ は $\mathbb{Q}$ の部分集合，すなわち $\mathbb{Z} \subset \mathbb{Q}$ である．よって，答えは (f) ．
    (5) すべての実数 $x$ について，$x \in \mathbb{C}$ が成り立つから，$\mathbb{R}$ は $\mathbb{C}$ の部分集合，すなわち $\mathbb{C} \supset \mathbb{R}$ である．よって，答えは (g) ．

    (6)
    ①　無理数は実数のうち，有理数でない数である．
    ②　①の定義より，集合 $A$ は集合 $\mathbb{R}$ から  $\mathbb{Q}$ を除いたものであるから，
    \[ A =  \mathbb{R} -  \mathbb{Q} \]

    よって，答えは ア：(r)，イ：(q)  ．

    補足①

    (6)は上の数の集合のベン図で表すと，次の図の塗りつぶされた範囲になります。

    補足②（記号について）

    集合の要素を表す $\in,~\ni$ や 集合どうしの包含関係を表す $\subset,~ \supset$ について補足します。
    まず，$\in,~\ni$ については「$a$ が集合 $S$ の要素である（集合 $S$ に属する）」 とき，
    \[ a \in S ~\mbox{あるいは}~ S \ni a \]
    と表します。

    次に部分集合についてですが，多くの人はベン図での包含関係で理解していると思いますし，それで問題はないと思いますが，数学的な定義について触れたいと思います。大学の数学（特に位相空間論）を学ぶと必ずでてくるので，理系の方は覚えてもいいと思います。
    集合 $R$ の任意の（すべての）要素 $x$ について，
    \[ x \in R  \Longrightarrow x \in S \]
    が成り立つとき，$R$ が集合 $S$ の部分集合であるといい，$R \subset S $ あるいは $S \supset R$ と表します。



      次回について

      第3講は「有理数と無理数①」を，順天堂大学・医学部の入試問題を用いて扱います。

      コメント

      コメントを投稿

      このブログの人気の投稿

      （数学基礎1-3）・有理数と無理数①

      イメージ
      数学の基礎のお勉強 第1章「命題と論証，数の世界」 第3講「有理数と無理数①」 「 数学の基礎のお勉強 」のシリーズの記事です。 またまた更新をサボってました… 記事の意図は上のリンク先を参照してください。 さて，最近Twitterで炎上してるこの画像はご存知でしょうか。 これについてのコメントは，私の愚痴が大半を占めるので一番下に回します。 ここでは， 正しい定義 を学びましょう。 前の記事 では，無理数が「実数のうち有理数でないもの」ということを最後に述べました。 では，有理数の定義は何でしょうか…？ 順天堂大学の過去問を用いて学びましょう。 問題 【2010年　順天堂大学・医学部　改】 (1)　有理数の定義を与えよ。 (2)　有理数の和・積はまた有理数であることを示せ。 (3)　命題の逆の裏を何というか。 (4)　$\sqrt{6}$ の定義を述べよ。 (5)　「自然数 $a$ が素数 $p$ の倍数であり，自然数 $b,c$ によって， $a=bc$ と表されるならば，$b$ または $c$ の少なくとも一方は $p$ の倍数である」という事実が知られている。この事実を用いて，$\sqrt{6}$ が無理数であることを背理法で証明せよ。 知識事項整理 本問では「有理数」についての問いの後，「無理数」についての問いが続くと言った構成です。 まず，有理数の定義は答えられるでしょうか。これ自体を問われなくても，有理数が何かわかっていないとできない証明問題もあります。例えば，有名問題である「$\sqrt{2}$ が無理数であること」の証明は有理数であると仮定して矛盾が生じることを使って示すわけですから，有理数の定義がわかっていないと解けませんよね。 さて，本題の有理数の定義ですが，なんとなく「分数で表される数」とわかっているとは思いますが，正しい定義を理解しましょう。 有理数とは， 「整数 $m$ と $0$ でない整数 $n$ を用いて，$\dfrac{m}{n}$ と表される数」 であり，これが(1)の答えとなります。符号については分子 $m$ を整数とすれば，正負どちらもふれられているので，$n$ は「自然数」としても特に問題はありません。ただし，大学に入ると自然数に $0$ を含め
      続きを読む

      2019年入試解答・第3弾「上智大・TEAP利用（理系）［1］」

      イメージ
      上智大学・TEAP利用（理系）[1] $\log x$は$x$の自然対数，$e$は自然対数の底を表す。 (1)正の実数$x$に対して \[ x - \frac{x^2}{2} < \log (1+x) < x - \frac{x^2}{2} + \frac{x^3}{3} \] が成り立つことを示せ。 (2)自然数$n$に対して \[ a_n = \left( 1 + \frac{1}{n} \right)^n \] とおく。 (i) 自然数$n$に対して \[ 1 - \frac{1}{2n} < \log a_n < 1 - \frac{1}{2n} + \frac{1}{3n^2} \] が成り立つことを示せ。 (ii) 不等式 \[e^{0.9} < a_n \] を満たす最小の自然数$n$を求めよ。 参考資料 永島先生ポイント集・ No.3240 感想 上智のTEAP利用入試は2015年入試から始まっていますが，理工学部の第1問では証明・論証問題が頻出です。また，2014年以前の理工学部A方式の数学でも，証明問題（特に公式の証明）が出題されていました。 （おそらく各大学での度重なる出題ミスの影響で）本年度入試より，多くの大学が入試の解答（例）や出題意図を公表するようになりました。上智大学の入試は全試験の解答・出題意図が既に公開されているので，本問の部分を抜粋します。 >>>>>>>>> 数列 $\left\{ 1 + \dfrac{1}{n} \right\}$ は自然対数の底 $e = 2.71 \cdots$ に収束するが, 本問ではこの数列がどの程度の速さで $e$ に収束するかについて考えることをテーマとしている。問(2)(ii) が主となる問であり，問(1)および問(2)(i)はそれを解くための誘導である。 (1)微分・積分を用いて, 関数の値の増減や大小を考察し, そこから不等式を論理的に導く力を問う。 (2)(i) 対数関数の性質を用いれば, ここで問われている不等式は問(1)の不等式の特別な場合であることがわかる。対数関数についての理解力, および洞察力を問う。 (ii)対数関数が単調に増加する関
      続きを読む

      数学の基礎のお勉強

      このシリーズについて ここでは，参考書に載ってはいるけど重要視されず，多くの学校や予備校の授業でスルーされてしまうところを扱っていきたいと思います。本記事には内容は書かず，リンクのみ貼っていきます。 「数学の基礎のお勉強」というタグをすべての記事につけています。 また，シリーズトップというタグをこのページに付けます。 リンク（記事が完成し次第，リンクを貼っていきます） 第1章…命題と論証，数の世界 第1講：命題とは何か 第2講：数の種類 第3講：有理数と無理数① 第4講：有理数と無理数② 第5講：有理数と無理数③ 構成（予定） 第1章…命題と論証，数の世界 数学IA範囲（で理解できると思います） 数学は「 論理的思考力 」を身に付けるための学問です。私立文系志望で数学なんかもうみたくないという人も見て欲しいところです。 正しく論証する・（数学の）議論をする ということを身に付けましょう。大学の数学では，かなり厳密に議論しますが，高校数学だと（教える人が）軽視している気がします。 この章の最後では 「無理数の無理数乗は無理数か」 という命題について考えます。ちなみに，真偽どちらかわかりますか？ （命題って何だ？っていう疑問にもお答えします。） 第2章…定義の確認と定理・公式の証明 「三角関数や微分係数とは何か？」 のような，数学の定義はきちんと理解していますか？分かっていないということは，それは 何だかよく分からないものを扱っている ということになります（この理解ができずに数学の授業が進んでしまうというのも数学が苦手になる一因です）。 「1/6公式」や「三角関数の合成」， 公式を鵜呑みにしていませんか？ （本当にそれらの公式が成り立っていることを確かめましたか？） 公式の証明を理解すれば，公式はただ暗記するものではないということがわかると思います（受験対策的には暗記した方がよい公式もありますが，それは数学本来の考え方ではありません）。
      続きを読む